兩組与多组獨立統計數據 變異數合併/Combined Variance /Pooled Variance

         工作每天都會看生產數據，測試數據量大且接近常態分佈，看看平均值 (u)與標準差(s)就可以大概了解整個數據的分佈狀況，99.7%的數據都會落在u±s內。

        隨著不斷的生產會有不同時間點的批次資料產生，數據會開始隨著製程偏移(process variation)數據會有偏移，例如有兩筆統計數據，可能是平均值不變一樣，標準差變大，或標準差不變但平均值偏移，或都不太一樣，那最後的平均值(u)與標準差(s)要怎麼得到。

        比較間單的方式就是全部的原始數據整在依據公式在從新計算一次，但如果統計一個季度或一整年數據量可能會超過10kk或更大，查了一下網路資料有查到合併變異數[1] 與[2] ，但公式驗證起來都有點問題沒辦法原本的數據。

平均值與標準差的定義 The Definition of Mean and Standard Deviation

        平均值Mean與標準差Standard Deviation的定義應該是高中數學就有教(但說實在我好像沒有什麼印象)。

        現在有一個母體數拆成兩筆測試數據，有每一筆的數量(m, n)，平均值(ux, uy)和標準差(sx, sy)，但沒有原始數據，但我們可以從定義之到整體的平均值(u)與標準差(u)的公式得到以下計算式，平均值(u)沒有什麼問題，可以從原本的平均值ux, uy與數量m, n計算得到，但標準差裡面還有個別的原始數據x1, x2...xm與y1, y2...yn，所以還要再整理一下。

         把變異數s展開，依序整理

繼續往後整理到𝑚×𝑢𝑥+𝑛×𝑢𝑦這個就是整個母體N的總和，也就是(𝑚+𝑛)×u，整理到這裡只剩下xi, yi平均數總和要跟已知的數據連結在一起。

可以從Standard Deviation的定義導出平方數總和與平均數之間的關係式如下。

最後整理一下就可以得到最後的結果，後來交叉查詢資料有看到YouTube上面的高中數學[3]有完整的推導，也可以參考一下。

這樣如果我們知道有分別兩筆統計資料，分別知道每筆資料的統計數量n, 平均數u與標準差std：

 

第一筆：n=15、平均數4.25、標準差STD 2.64

第二筆：n=12、平均數14.25、標準差STD 2.64

只看這兩筆資料的平均數與標準差可以畫出分佈圖如下，計算合併後的平均數也很直觀:

u=[1/(15+12)]*[15*4.25+12*14.25]

然後可以透過公式計算出合併後的方差與標準差為:

方差: 31.71

標準差: 5.63

如果把合併後的統計資料與原本兩個資料放在一起比較就會類似下圖分佈。

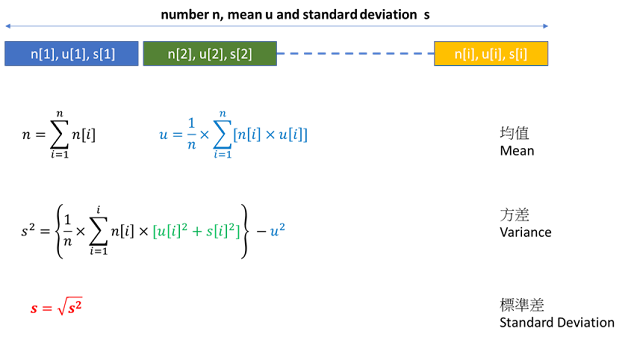
其實從公式中你也可以達到多筆統計資料的合併公式，為了方便呈現公式這裡改成第一筆資料數量n[1], 平均數為u[1], 標準差為s[1]，所以第二筆為n[2], u[2], s[2]以此類推，合併後的公式可以兼化成如下。

參考資料

[1] Wikipedia, Pooled variance

https://en.wikipedia.org/wiki/Pooled_variance

[2] eMathZone, Combined Variance

https://www.emathzone.com/tutorials/basic-statistics/combined-variance.html

[3] YouTube, 高中數學免費線上學習網,  “B2---4--1----範例9----已知兩組資料的平均與標準差求合併後的平均與標準差”

https://www.youtube.com/watch?v=BxyGU1hwtLU