Introduction
功率放大器在學習的過程,從電子學一直到微波工程,有時候對為什麼是Power Matching不是共軛匹配? 負載線理論? 為什麼Voltage Sweep是兩倍的Vcc (twice Vcc)? 最高效率有時候是25%有時候50%? 常常搞迷糊,今天抽空把之前弄迷糊的地方寫下來。
功率放大器就是.....一個放大器,功能目的就是把輸入訊號放大,傳遞最大功率輸出,因為行動裝置距離基地台距離可不是家裡擺一台AP router這麼近,要能夠把訊號不失真的傳送出去,就需要功率放大器,這也是每次iphone出新手機,財經新聞就會把功率放大器概念股拉出來講一次。
一個功率放大器最重要的指標就是輸出功率可以到多大,1W, 2W...10W然後效率與線性度,線性度就是要放大等比例把輸入訊號放大,接收端才不會上傳一張照片卻失真變成金城武。
如果是用在行動裝置上面ex iphone,電流表現尤其重要,這關乎手機是否發熱與電池續航力,在真實世界裡行動裝置在傳輸功率是一個動態的過程,也就是說在訊號不好的時候會輸出最高功率1W 30dBm,但是大部分時間訊號好的時候可能只有操作27dBm或更低。
一個功率放大器最重要的指標就是輸出功率可以到多大,1W, 2W...10W然後效率與線性度,線性度就是要放大等比例把輸入訊號放大,接收端才不會上傳一張照片卻失真變成金城武。
如果是用在行動裝置上面ex iphone,電流表現尤其重要,這關乎手機是否發熱與電池續航力,在真實世界裡行動裝置在傳輸功率是一個動態的過程,也就是說在訊號不好的時候會輸出最高功率1W 30dBm,但是大部分時間訊號好的時候可能只有操作27dBm或更低。
以這樣的應用場景,應該挑選或設計一顆功率輸出功率大於30dBm的功率放大器,但又怕最後設計天線效率不如預期,所以應該要抓一點點Margin,但要抓多大的規格呢? 多個1dB or 2dB or 3dB呢?
那不就選用市面上能輸出最高功率的放大器不就好了,這就跟買車一樣,到底要買100匹馬力,還是買300匹馬力輸出的汽車道理蠻像,讓我娓娓道來。
線性功率放大器Linear RF Power Amplifier (Class A)
一般常見的RF Power Amplifier如下圖,這是一個common emitter架構的功率放大器,無論是BJT or FET,電晶體在這裡的作用可以視為一個電流控制器,白話一點就是水龍頭,控制訊號iB是控制電流的開關。
這裡假設RF Choke Inductor與AC coupling電容都非常大,所以可以簡化成右邊架構,最後流過電晶體的電流iC會從負載R流過電晶體R,這時候負載得到的功率用歐姆定律 I^2*R就可以得到。
因為是電晶體本身只能一個開關用來控制流過電流的大小,如果輸入訊號是一個正弦波訊號AC or RF訊號,那一開始就要給一個偏壓電流讓電流Iqc這時候,這樣輸出電流波型才會上下對稱,也就是處在線性操作 (Linear Operating)
負載線理論Load-Line 最大線性功率輸出Ropt
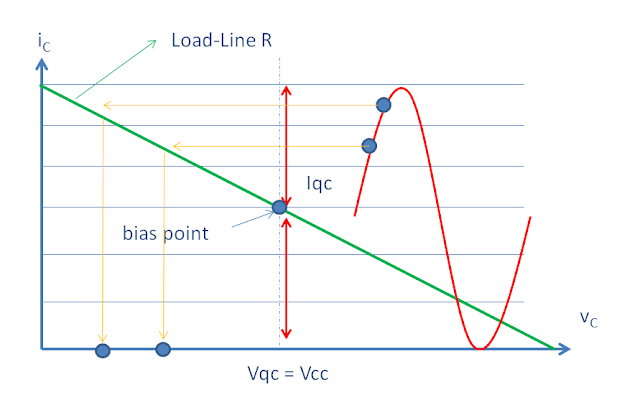
負載線理論是功率放大器用來決定輸出負載R是幾歐姆? 底下是一個完美IV Curve, X軸是Collector電壓vC,Y軸是流過電晶體的電流iC,偏壓點bias point也就是只有DC狀態的初始點是
1. Vqc: Supply Voltage Vcc
2. Iqc : 偏壓電流IB所對應的Iqc
iCC流過負載R,負載上面的電壓輸出vC就會沿著負載線移動。
電流輸出限制Current Limitation
負載線理論Load Line Theory主要要討論的是不同的負載會限制電流的輸出大小, 下圖虛線R' < R,所以電流往上掃的過程需要更大的電流才會對應相同的電壓輸出,但電流往下也就是電晶體越關越緊越關越緊到最後完成鎖死沒有電流的情況下,可以看到以下這個例子電流輸出波型會不對稱,輸入訊號是弦波但輸出訊號下半部被截止,也就是所謂的失真。
電壓輸出限制Voltage Limitation
我們把R'設定比原本的R來的大,這時候可以觀察到電流往上增加的過程,Vc在降低,但降到最後會碰到vC=0的這條線,因為電晶體本身只是控制電流大小,當你VBE兩端電壓都為零的時候,沒有電位差是不會有電流的,所以這時候電流會被"截止斷頭"造成電流波型失真。
最佳負載線Ropt與偏壓點Vqc and Iqc
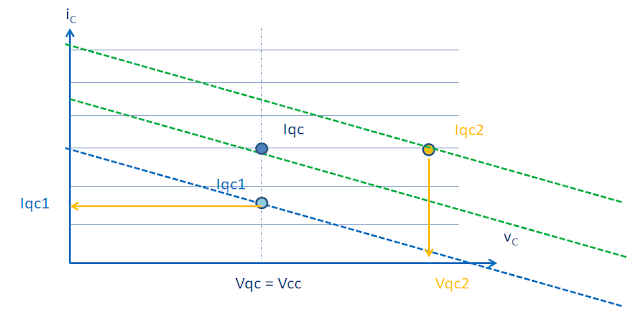
一個線性功率放大器的操作,電流不希望被截止失真,但是以上的例子可以看出來負載線R與偏壓點Vqc, Iqc是互相綁再一起,比方說上面電壓輸出限制造成電流頭頂截止的狀況,可以透過調整bias point上電流的swing上下對稱。
1. 拉高Vqc,增加電流往上擺幅太大被左邊電壓0V邊界限制住。
2. 降低Iqc,降低電流往下擺幅達到下上對稱的結果。
不更改負載R的條件下我們可以透過更改偏壓點的負載來達成最佳性線偏壓點,但可以看到這兩個最大的輸出線性功率是不一樣的。會相差20log(Vqc2/Vqc),如果Vqc=3V, Vqc2=6V最大線性輸出功率就會差到6dB。
決定最佳負載線,最高電壓2倍Vcc?
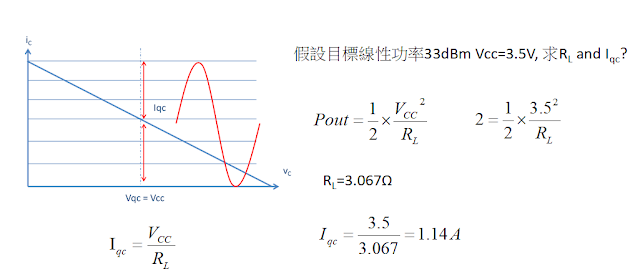
實際應用的時候,電壓Vcc已經被決定例如3.5V, 5V, 12V, 24V.....,這然後再決定線性輸出功率多少,就可以算出Iqc和Ropt,例如系統電源為3.5V, 輸出功率為33dBm,因為輸出要對稱,這邊的考量都是因為輸出要是線性輸出,所以當你Vcc決定,你的最大高壓Swing就會是兩倍Vcc,這一點與有些電子學用Transformer所以有兩倍輸出的概念不太一樣,因為電壓Waveform實際會超過2倍,但因為沒有電流,所以這個輸出功率是虛,並不是說最Voltage Swing只能兩倍Vcc喔。
所以我們可以計算用Pout推算出RL,因為電流要對稱輸出,所以可以計算出Iqc的值。
最高輸出效率
從電子學就有學過Class A Power Amplifier,但你可能有印象最Class A PA高效率Maximum Efficiency為50%,但使用Transformer後會變成50%。這中間的差異主要是來自RF輸出功率,剛剛上面提到最高線性輸出會是2倍的Vcc,但如果是電子學一開始會用電阻當負載,也就是說最高的Voltage Swing只能到Vcc而非2xVcc,但消耗的總DC功率是不變的 IqcxVcc.
所以在最高線性輸出2W的時候可能拿到50%的效率,但如果輸出功率退到27dBm,因為總消耗功率沒有變,效率就會跟著降低到12.5%。
不同負載線輸出效率比較
一樣的Vcc條件下,把輸出功率設定到30dBm然後可以計算出一組新的RL與Iqc,可以看到因為輸出功率比較低,但是輸出的Voltage Swing是不變的(最大一樣是2xVcc),這邊在提醒一下,2xVcc是不失真情況下最高的輸出,並不是說以下的IV curve限制了輸出電壓只能2xVcc。
如果一樣是退回27dBm下操作,可以看到Max Pout 30dBm的效率就會比Max Pout 33dBm放大器的效率好,這理由也很簡單就是Iqc降低整體DC工耗降低導致。
這動作其實跟現在很多小cc的汽車道理很像,買了馬力輸出500hp的汽車,但實際高速公路只有用到40-60hp,耗油只是理所當然的事情。
功率放大器的省電技巧,動態Bias Point
就跟汽車省油技術一樣,例如大家有聽過i-VTEC正時可變汽門技術或渦輪增壓Turbo技術一樣,在小功率輸出的時候我把Iqc降低一點讓電流Swing剛好滿足當時線性功率輸出的要求,這樣就可以在小功率輸出的時候節省不必要的DC功耗。
把可調Iqc的概念放到套用在剛剛33dBm輸出的功率放大器上面,一樣退到27dBm操作的時候,效率就可以從原本12.5%拉高到25%.
一樣的作法我在在比較一次RL設計給33dBm與RL設計給30dBm,在可調Iqc的條件下,套用在RL設計給30dBm的功率放大器上面,還是可以得到比較明顯的改善。
功率放大器的省電技巧 II
聰明的你一定想到,Class A最佳線性輸出效率是50%,所以如果同時調整Vcc和Iqc這樣不就是可以達到效率一直處於50%的甜蜜位置嗎? 如下圖所示。
恩...以上面整個模型沒錯,如果系統可以任何調整Vcc和Iqc而且IV curve也是理想的,但現實是很殘酷的。
讓我們回到現實元件的IV curve,本身並非線性,所以實際可以操作的Vcc和Iqc範圍是有限制的,而且如果靠Buck來降低Vcc,效率通常會直接損耗在Buck身上。
剛剛提到的都是調整bias point,但RL呢? 這其實也是目前實際在使用的技術,常見的Antenna Tuning (Capacitor Array)就是這樣的功能。
/
結論
上面提到的都是很理想的模型,你也知道實驗室油耗數據跟上路實測都有差異,只是實際限制比較多,並不能真實達到理論的偏壓操作點與輸出功率。
其實可以看到,選用功率放大器要看輸出功率與生產的容忍變異來決定用多大的功率輸出,並不是越高越好,就像買車一樣,剛剛好用的車最省油,但是如果你就是要馬力或功率輸出有多大就多大,不在意油耗或電流,那是另外一種選項。