在現實(Real)的世界裡，意識虛幻(imaginary)的存在, 現代通訊基礎傅立葉轉換Fourier Transform

i (imaginary) 虛數

        黃昏，非日非夜的時段，世界的輪廓變得模糊，可能看到非人之物的時段。七月普渡的時候，有沒有想過有沒有你看不到事物正在供品前面，每次數學重大的突破，都為了人類科學往前進一個世代，現在無論學任何工程學科，都一定會處理複數complex a+bi，i (imaginary)，虛數的出現也才推進整個科學往後進步， 虛數在學習過程都習慣它的存在，但你如何在現實的時域領域中觀察到到的存在?
   

歐拉Euler's Formula

        學電子電機的一定會用過示波器Oscilloscope，底下是一個常見的cos(wt)與sin(wt)訊號，無論任何訊號就是時間與某個東西的變化，底下弦波就是時間對電壓的變化，但你量的到的都是時數訊號Real Part, 但Euler's formula 歐拉公式卻串聯了實數與虛數之間的關聯。

時域訊號

        歐拉公式Euler's Formula跟我們講cos(x) or sin(x) 可以用寫成如下訊號，跟你講說一個實數(Real)骨子裡面帶有i (imaginary) 虛數成分，其實一開始學i的時候就跟你說i的定義是i平方會等於-1，-1是個實數Real但是你卻無法在實數座標軸上面點出i一樣，不覺得這個跟陰陽兩界很像嗎? 說不定它存在但只是生活在現實世界(Real)的你觀察不到虛無世界的數，但透過特別的方法比方說觀落陰某種轉換過程可以讓你間接觀察到它。

最美的数学公式是哪个？自然数是如何拓展出复数的？李永乐老师讲欧拉公式（2018最新）

傅立葉Fourier Transform

        傅立葉轉換Fourier Transform是工程數學上一個很重要的工具，無論是影像處理或通訊領域，沒有它你手上的iPhone就會變成一台影音撥放機iPod，Fourier它是一個一對一的線性轉換公式，一維的x軸上取樣單位如果是時間軸time, u就是時間的倒數1/T, 也就是頻譜f的概念，但然如果是距離呢? 什麼是距離的倒數呢? 比方說波長的倒數光學系統就很常用到，當然拓廣到二維那又是另外一個與我們生活息息相關的影像處理基礎了。
     

        但數位是無法處理連續的訊號，紀錄下來的任何資料都是離散(Discrete)訊號，所以會常看到DFT離散傅立葉轉換，其實生活中目前大部分的訊息都是離散的資訊，比方說數位音樂，影片，股市指數.....ㄟ 都是離散的訊號。你一小時記錄一次，那你就可以1分鐘紀錄一次，那一分鐘記錄一次那為什麼不1秒鐘記錄一次..........所以在怎麼細分下去記錄在多資訊都是離散的資料。

        如下圖示個離散訊號取樣的過程，離散傅立葉轉換是個1對1維度的轉換，所以右邊的取樣維度為N個點，轉後也會得到N點的F(u)資料，而且轉換過程F(u)會是以複數complex的形式出現。

DFT

Negative Frequency 負頻概念

        DFT轉換中如果 x為時間，也就是f(x)為取樣的數據，傅立葉轉換F(u)就是頻譜函數，另外因為DFT離散傅立葉轉換是複製取樣訊號為其中一個週期訊號，從Euler's Formula可以知道整個展開中的根為Cos or Sin，三角函數Sin or Cos經過180度後，會相差一個正負號。所以在表示式方面常會看到有人把它最以下的轉換方便閱讀。

          以常見到的cos與sin訊號進行Fourier Transformation，可以得到以下資訊，可以看到Cos or Sin都會看到轉出負頻率的成分，而且在數學計算上面頻譜為複數Complex形式 (a+bi)，這也是一個在學習工作工程困擾我的過程，因為一般頻譜分析儀都是量測大小，看不到所謂的負頻成分與複數形式，那種看不到但感覺好像存在的東西真的令人感到困惑。
        1. Negative Frequency
        2. Complex Spectrum

        其實Sin or Cos的例子可以看出來，在只有實數(Real)的訊號下，會得到虛數的頻譜，但傅立葉轉換剛剛前面提到是個線性過程，因為我們只能量到真實的訊號(Real Part)去進行運算，可以得到數學上有虛部成分的頻譜訊號，反過來如果我們先把頻譜訊號固定好，再利用轉換過程得到時序訊號呢?

OFDM/IFFT 通訊概念

        FFT/IFFT是Inverse/ Fast Fourier Transform的縮寫，它是一個DFT的特例型，所以基本上它就是DFT，只是N必須要為2的次方例如2, 4, 8, 16.....4096..2^N等等，這也是現代常見通訊技術的基礎LTE, WiFi 802.11ac/ac, ADSL，都是基於OFDM調變技術，而OFDM就必須要往下談到Inverse Fast Fourier Transform 。
        學通訊都知道QAM的調變技術，在相同的Symbol Rate下可以增加傳輸量，把上面計算的時域訊號經過計算....可以得到頻譜訊號，頻譜訊號又是Complex格式，我們可以利用這個特點來進行QPSK的調變(16QAM, 64QAM, 256QAM也是一樣的理論)，例如我們要傳送11的訊號就把f1的頻譜設定為1+0i, 要增加資料量我們在塞入一個頻譜-f1，比方說要傳送10的訊號就設定為0+1i，這樣我們就有所謂的數學上或在電腦上的頻譜資訊，有虛數存在資訊。

QAM

        然後再利用Fourier Transform把頻譜資訊轉換成時序訊號，這樣我們就可以利用DAC依序把資料刻出來，就像CD/MP3一樣把存放在電腦的資訊轉換出來，但這邊出了一些小問題，那就是轉出來的訊號有imaginary part，但是真實的世界只能接受真實的訊號，或你要怎麼把需部訊號在真實的世界表現出來?

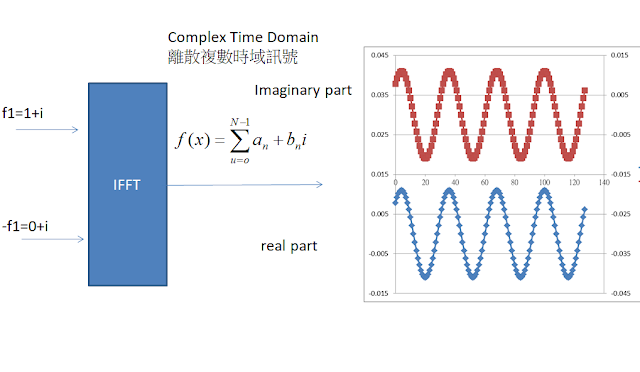Complex Time Domain Signal

        事實上沒有辦法，兩個維度的訊號就需要兩個頻道(Channel)來傳送，所以可以這麼傳送，把兩個訊號獨立出來傳送，在接收端分別在解回來。

IQ modulation

        但實際上不會這麼做，如果是拉兩條獨立的電纜線cable還可以，但無線通訊就不太實際了，所以接下來就是大家不陌生的IQ modulation, 透過Sin(wt) and Cos(wt) 彼此正交的特性，將兩個獨立的訊號載到相同的頻率上面再透過一樣的方式接調下來。

Conclusion

         To see is to believe, 到最後你會發現，在真實的世界裡你沒辦法產生複數的時域訊號，透過一些轉換(數學)你可以了解到它的存在，或許就跟很多科幻電影講到，二維生活的螞蟻無法意識到三維的世界，三維世界的我們無法感受多維的世界觀一樣，現實的訊號無法察覺到虛數的存在。

參考連結:

https://www.dsprelated.com/showarticle/192.php
http://www.panoradio-sdr.de/ssb-demodulation/
http://rfic.eecs.berkeley.edu/ee242/pdf/Module_2_1_RxArch.pdf